LOS PRESOCRÁTICOS

Fue un grupo de filósofos griegos que precedieron a Sócrates. De ahí su nombre.  La filosofía Presocrática dio inicio en una colonia griega situada en Asia Menor, en lo que hoy se conoce como Turquía. La escuela de Mileto, fue la primera en romper con ese pensamiento en función de lo mítico, lo sobrenatural y dar paso a un pensamiento más especulativo, inclinado a la razón. Tales de Mileto, su principal representante y fundador, fue el primero en adoptar dicho pensamiento. Él comenzó a estudiar la naturaleza (physis) y se planteó dos cuestiones básicas relacionadas con la multiplicidad de seres y el cambio. Para contestar dichos cuestionamientos, él definió un nuevo concepto que le permitió explicar todo lo que sucedía en la naturaleza. Ese nuevo concepto lo denominó Arjé o principio de todas las cosas. Este concepto fue utilizado reiteradas veces por sus sucesores y fue cambiando con el paso del tiempo.

TALES DE MILETO

 Para  Tales de Mileto, dicho Arjé fue el agua. En el campo de las matemáticas, Tales de Mileto fue un gran geómetra. Dicen que, durante un viaje a la antigua ciudad del Nilo, a saber, Egipto logró medir la altura de las pirámides usando un peculiar método de comparación de sombras. También, en el campo de la astrología, fue capaz de predecir un eclipse de sol que tuvo grandes repercusiones para la época. 

PRIMER TEOREMA DE TALES

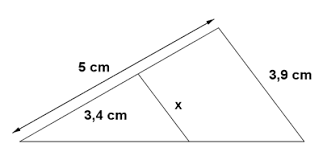
EL teorema de Tales se considera el teorema fundamental de la semejanza de triángulos y establece lo siguiente: Toda recta paralela a un lado de un triángulo, forma con los otros dos lados o con sus prolongaciones otro triángulo que es semejante al triángulo dado.

Ejercita tus habilidades (en Geogebra) con los siguientes ejercicios:

APLICACIÓN INTERACTIVA DEL PRIMER TEOREMA DE TALES EN GEOGEBRA:

https://ggbm.at/nJ2DFKy6

SEGUNDO TEOREMA DE TALES

Sea B un punto de la circunferencia de diámetro AC y centro "O", distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo donde <ABC = 90º.

APLICACIÓN INTERACTIVA DEL SEGUNDO TEOREMA DE TALES EN GEOGEBRA:

https://www.geogebra.org/m/jk3hxuvj

LA PIRAMIDE DE KEOPS

El método que utilizó Tales de Mileto para calcular la altura de la Pirámide de Keops es lo que conocemos como Teorema de Tales (parece obvio por qué se llama así).

El siguiente esquema nos permite ver el problema en cuestión y cómo calculó Tales la altura de la pirámide clavando su bastón en la arena.

La sombra es la región donde no dan los rayos del sol. Se supone que los rayos que inciden en la pirámide y en el bastón son paralelos (consecuencia de la gran distancia que separa al Sol de la Tierra) y el bastón está clavado perpendicularmente al suelo.

De esta forma, los ángulos de los dos triángulos que observamos en la figura son iguales entre sí y, por tanto, dichos triángulos son semejantes.

En dos triángulos semejantes, se cumple que sus lados homólogos son proporcionales.

En nuestro caso, se cumple que:

Supongamos ahora que a una hora determinada del día, la sombra de la pirámide medía 280 metros, la sombra del bastón medía 2,87 metros y dicho bastón era de 1,5 metros. Según lo que hemos visto antes, tendríamos que:

De donde obtenemos:

Que es el valor aproximado que tenía la pirámide de Keops en la antigüedad (actualmente tiene 136,86 m).

Dejando de lado la escuela de Mileto, nos enfocaremos en otra colonia griega, situada en la actual península itálica. La escuela de Pitágoras, fue de gran relevancia para el campo de las matemáticas. Pitágoras, su fundador, comenzó a forjar un camino más ameno para las matemáticas. Aunque Tales de Mileto ya había incursionado en dicho campo, sus aportaciones se basaron, más o menos, en la observación y no se preocupó por una demostración más formal. En cambio, Pitágoras y sus discípulos dieron un gran paso en la construcción de un esquema, de unas herramientas, que le permitieron dar rigor a todos sus resultados. Para ellos, esos símbolos que interpretamos como números fueron de gran importancia e incluso llegaron a verlos con otros ojos, es decir, le dieron ciertas características que actualmente carecen de importancia. Por ejemplo, el número 4 se consideraba símbolo de justicia y solidaridad. Entre todos ellos, el número 10 fue quizás el más importante. Dicen que durante las ceremonias de iniciación siempre se juramentaba ante dicho número. Era un número muy sagrado. De ahí, es claro que su Arjé eran los números. Cabe destacar que dicha escuela creía fielmente que todo se podía representar por medio de los números enteros, pero cuenta la leyenda que uno de sus discípulos usando el teorema de Pitágoras, a saber, el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de sus catetos, encontró algo aterrador, algo que carecía de nombre, algo que logró culminar de manera estrepitosa esa idea de representación. Un número irracional, a saber, raíz cuadrada de dos.

Dejamos para el final, y sin darle menos importancia, la escuela Eleática. Parménides, su fundador, tenía ideas bastante radicales, ya que él creía que la realidad era única, se negaba al cambio, es decir, el cambio y el movimiento no pueden existir, son simples ilusiones. Para él, el principio no era otro que el Ser, lo que es, es y lo que no es, no es. Uno de sus discípulos favoritos, a saber, Zenón de Elea fue capaz de enunciar varias paradojas que hicieron titubear a más de uno acerca de la idea de cambio y movimiento. Por ejemplo, si una persona quería ir de un punto A a un punto B, debía pasar por la mitad de dicha distancia, y para llegar a la mitad debía pasar por la mitad de esa mitad, y así sucesivamente. Entonces era natural preguntarse, ¿Será que en algún momento comenzaremos a movernos? Lo que pretendía Zenón con esas paradojas era defender las ideas de su maestro Parménides. Cabe resaltar, que dichas paradojas dieron origen a ideas muy recientes como la idea del infinito.

Para concluir, diremos que las aportaciones de los presocráticos fueron muy contundentes. Desde la filosofía, con su idea del Arjé o principio único que trataba de esclarecer el origen de todas las cosas, hasta las matemáticas con la implementación de pruebas rigurosas que daban cierto rigor a sus resultados y a la creación de otros con mayor precisión. 

PARADOJAS DE ZENÓN

Otro hecho epistemológico importante se le atribuye a Zenón de Elea y sus paradojas. Con ellas, Zenón pretendía demostrar la unidad del ser, la cual era indivisible en el espacio, pues si lográramos dividir al ser una vez, pues dicha división también es divisible, y estas nuevas fracciones también lo serán y así en una serie que se sigue de manera infinita. Es por esto que el ser puede ser infinitamente grande o pequeño a la vez, lo cual va en contra de lo que ya se conocía o aceptaba en aquella época. Sin embrago, la intuición poco demuestra en cuanto a rigor, mientras que las matemáticas han demostrado un orden usando el rigor de la lógica de las formas y principios del pensamiento humano. Por ello, no es de extrañarnos que la solución a dichas paradojas resida en el dominio de las matemáticas. Daremos algo de contexto, también mediante una historia:

Aquiles, el atleta más veloz, capaz de correr los 100 m. en 10 segundos, no podrá alcanzar a una lenta tortuga, diez veces menos rápida que él. Ambos disputan una carrera, concediendo Aquiles una ventaja de 100 m. a la tortuga. Cuando Aquiles ha cubierto esos 100 m., la tortuga se ha desplazado 10 m. Al cubrir Aquiles esos 10 m., la tortuga se ha desplazado 1 m. Mientras cubre ese metro que le separa de la tortuga, ésta ha recorrido 0'1 m. Y así indefinidamente.

Así, Aquiles debe cubrir infinitos trayectos para alcanzar a la tortuga. Por lo tanto, Aquiles deberá cubrir una distancia infinita, para lo cual necesitará un tiempo infinito. De tal manera que el desgraciado Aquiles nunca alcanzará a la tortuga.

Es evidente que esta paradoja, bajo una apariencia de razonamiento correcto, esconde algún fallo. Todos sabemos que Aquiles debe alcanzar a la tortuga. Pero se tardó 24 siglos en desvelar por completo, gracias a la Teoría de Límites, cuál era el fallo: la suposición de que infinitos trayectos deben sumar una distancia infinita y necesitan un tiempo infinito no es correcta.

La historia deja en evidencia el surgimiento de un nuevo concepto, algo inconcebible para la época, a saber, la noción de infinito. Estas paradojas, de alguna forma, sacudieron las bases de las matemáticas más recientes. Llegaron cuestionamientos como: ¿Existen infinitos más grandes que otros? ¿Pueden dos conjuntos infinitos A y B tener la misma cardinalidad, esto es, tener la misma cantidad de objetos? Estas nociones despertaron cierto interés en algunos matemáticos, a saber, Bertrand Russell mostró que los argumentos de Zenón, de alguna manera, sentaron las bases de casi todas las teorías del espacio, del tiempo y del infinito, construidas desde su tiempo hasta ahora. Demostró que la serie de puntos de una línea es un continuo matemático, por ello es que son inexistentes los momentos consecutivos o el número de momentos que interfieran ad infinitum en los momentos dados, y que la paradoja de Zenón tiene solución si se incluye el tiempo como una variable que Zenón no tomó en cuenta para su resolución. También, Georg Cantor y su teoría sobre los infinitos, la cual ha llegado a ser de notable importancia en el campo de las matemáticas e incluso es fundamental en las bases de la lógica y la filosofía de la matemática, ya que a partir de Cantor se admite en la teoría de conjuntos, como un axioma, que existen conjuntos que pueden ponerse en correspondencia biunívoca con uno de sus subconjuntos estrictos. En tales conjuntos infinitos ya no es cierto que el todo es mayor que sus partes. Así, dados más de un conjunto, podemos comparar la magnitud de dos conjuntos diferentes, por ejemplo, si A y B son apareados de tal manera que a todo elemento de A le corresponda un único elemento de B y viceversa, se dice que entre ellos existe una correspondencia biunívoca y dichos conjuntos se dice son equivalentes.

AQUILES Y LA TORTUGA

LA DICOTOMÍA





LA FLECHA CAMINANTE

El teorema de pitágoras

Para entender un poco mejor la historia del teorema de Pitágoras es necesario conocer que está relacionada con un gran número de descubrimientos y de avances importantes a lo largo de los años, sin embargo el origen de pitagoras fue conocido como Teorema de Pitágoras gracias a la aportación de Pitágoras, quien tras años de estudio consiguió aplicar su teoría de la proporcionalidad entre los lados de un triángulo rectángulo.

Así pues, la historia de Pitágoras se resume en que fue un filósofo y matemático de la antigua Grecia que contribuyó de manera significativa en el avance de las matemáticas, la filosofía y la geometría. El filósofo fue el impulsor de la escuela pitagórica en el siglo VI a.C. y gracias a la ayuda de los pitagóricos, aquellos que pertenecían a la escuela, consiguió el descubrimiento de lo que hoy en día conocemos como el Teorema de Pitágoras.

Actualmente, no podemos asegurar con certeza que el verdadero origen del Teorema de Pitágoras pertenezca en su totalidad a Pitágoras, pero lo cierto es que la propiedad de la proporcionalidad de los triángulos rectángulos fue un estudio realizado por Pitágoras, así como su consiguiente demostración y aplicación.

Para aplicar su teoría, Pitágoras elaboró una ecuación conocida como la fórmula del Teorema de Pitágoras mediante la cual se expresaba que la suma del cuadrado de los lados menores de un triángulo rectángulo, es decir los catetos, era igual al cuadrado del lado, la hipotenusa, mayor del mismo triángulo. Gracias a ésta fórmula surgió el origen de la demostración del Teorema de Pitágoras consiguiendo aportaciones de grandes filósofos como la demostración del teorema de Pitágoras por Euclides y se reveló la proporción que guardan este tipo de triángulos.

JUEGO INTERACTIVO:

https://scratch.mit.edu/projects/294108655/