Epistemología en el sistema de numeración Hindú-Arábigo
La civilización árabe recibió el sistema de numeración de la civilización hindú, pero los árabes fueron quienes aplicaron métodos, reglas u operaciones a estos números para así implementarlos en la Economía, Agricultura, es decir llegaron a aprovechar este sistema de numeración para el uso de la vida cotidiana y así con ella poder hacer la vida mas fácil; ademas no solo se quedaron con eso para ellos sino también los llevaron a otros lugares como en Europa donde allí facilitó mucho más la economía para todos los ciudadanos.

Después de haber explicado la notación hecha por Al-Khawarismi, mostraremos el contenido de este libro; es decir que ecuaciones se trabajaron:
Contenido:
La llegada del sistema de numeración Hindú al Islam
La llegada del sistema de numeración Hindú-Arábigo a Europa
Algoritmi De Numero Indorum
- Expone detalladamente el sistema de numeración utilizado por los indios.
- Muestra o explica como realizar cálculos numéricos como los que ahorita conocemos como la suma, resta, etc
Hisab Al-yabr Wa'l Muqqabala
Antes de mostrar el contenido vamos a explicar como los árabes definen las ecuaciones:- Las variables a,b,c son números enteros positivos.
- Las Raices eran representadas como bx.
- Los cuadrados eran representados como ax
- La palabra Mal en notación moderna significa x²
- La palabra Kab en notación moderna significa X3

Después de haber explicado la notación hecha por Al-Khawarismi, mostraremos el contenido de este libro; es decir que ecuaciones se trabajaron:
Contenido:
TIPOS DE ECUACIONES:
- Raíces iguales a cuadrados: bx = ax
- Raíces iguales a números: bx = c
- Cuadrados iguales a números: ax = c
- Cuadrados y Raíces iguales a números: ax + bx = c
- Raíces y Números iguales a cuadrados: bx + c = ax
- Cuadrados y Números iguales a Raíces: ax + c =bx
Rubaiyat
- Es una recopilación de hasta un millar de cuartetos que hablan sobre la naturaleza y el ser humano.Esta obra fue hecha por el matemático,filosofo y poeta Omar Khayyam.
- Contiene un profundo sentido humano que canta los deleites del amor y los goces de la vida, que con las transposiciones de la amargura y optimismo, conforman el carácter del individuo acentuado en su realidad.
Cuarteto:
No busques prolongar la simpatía que alguien te inspiro.
Antes de estrechar la mano de un hombre,
piensa si ella no te golpeara un día.
Trigonometría
 La matemática árabe y, en particular, la trigonometría, se
alimentó fundamentalmente de la Grecia clásica por un lado y de la India por el
otro. De hecho, la mayor parte de los trabajos hindúes fueron no sólo
traducidos por matemáticos árabes y persas, sino que también extendieron muchos
resultados, alejando la trigonometría de las meras aplicaciones, que era lo que
fundamentalmente se hacía hasta esos momentos.
La matemática árabe y, en particular, la trigonometría, se
alimentó fundamentalmente de la Grecia clásica por un lado y de la India por el
otro. De hecho, la mayor parte de los trabajos hindúes fueron no sólo
traducidos por matemáticos árabes y persas, sino que también extendieron muchos
resultados, alejando la trigonometría de las meras aplicaciones, que era lo que
fundamentalmente se hacía hasta esos momentos.
Epistemología en la trigonometría
Una aplicación que le dieron fue a la sombra generada entre el sol y una varilla ubicada de forma horizontal, de esta forma se pusieron en contacto con las funciones trigonométricas.
Los árabes quedaron tan fascinados con esto que siguieron investigando hasta que se dieron cuenta que servia o daba un gran uso para calcular la altura de algunos objetos tan grandes que de manera empírica no la podrían calcular y de allí llegaron a las funciones trigonométricas que ahorita conocemos como tangente, secante y entre otras.
Una aplicación que le dieron fue a la sombra generada entre el sol y una varilla ubicada de forma horizontal, de esta forma se pusieron en contacto con las funciones trigonométricas.
Los árabes quedaron tan fascinados con esto que siguieron investigando hasta que se dieron cuenta que servia o daba un gran uso para calcular la altura de algunos objetos tan grandes que de manera empírica no la podrían calcular y de allí llegaron a las funciones trigonométricas que ahorita conocemos como tangente, secante y entre otras.
Teoría de Números
Comprobación de la multiplicación:
Para comprobar una multiplicacionón utilizaban la regla para "expulsar los nueves". Esta regla es un método originalmente indio para comprobar la suma y la multiplicación.
Utiliza la propiedad bien conocida de que la suma de los dígitos de cualquier número natural cuando se divide por 9 da el mismo resto que cuando el mismo numeros se divide por 9.
Ejemplo:
Para comprobar que el producto de 436 por 659 es 287.324:
1. Sumar los dígitos de 436 para obtener 13, cuyos dígitos suman 4.
2. Sumar los digitos de 659 para obtener 20, cuyos dígitos suman 2.
3. Sumar los dígitos del producto 287.324 para obtener 26, cuyos dígitos suman 8.
Por lo tanto, al "expulsar los nueves" queda restos de 4, 2 y 8, respectivamente, como 4*2=8, la multiplicación probablemente sea correcta.
Utiliza la propiedad bien conocida de que la suma de los dígitos de cualquier número natural cuando se divide por 9 da el mismo resto que cuando el mismo numeros se divide por 9.
Ejemplo:
Para comprobar que el producto de 436 por 659 es 287.324:
1. Sumar los dígitos de 436 para obtener 13, cuyos dígitos suman 4.
2. Sumar los digitos de 659 para obtener 20, cuyos dígitos suman 2.
3. Sumar los dígitos del producto 287.324 para obtener 26, cuyos dígitos suman 8.
Por lo tanto, al "expulsar los nueves" queda restos de 4, 2 y 8, respectivamente, como 4*2=8, la multiplicación probablemente sea correcta.
Curiosidades sobre los números impares:
Si se colocan números impares sucesivos en una tabla cuadrada, la suma de los números será igual al cubo del lado; la suma de los números que llenan el cuadrado será la cuarta potencia del lado. Las diagonales del cuadrado al sumarse obtenemos:
Las diagonales del cuadrado al sumarse obtenemos:9+17+25+33+41=125
1+13+25+37+49=125
Note que 125 es el cubo de 5 que es la cantidad de filas(o columnas) de sucesiones de números impares, y la suma total de los números del cuadrado es 625 que es la cuarta potencia de 5.
 Ahora, si se colocan números impares sucesivos dentro de un tríangulo, la suma de los números de una fila es igual al cubo del numero de la fila.
Ahora, si se colocan números impares sucesivos dentro de un tríangulo, la suma de los números de una fila es igual al cubo del numero de la fila.La disposición tríangular de los números impares del 1 al 30 se muestra en la siguiente figura. Se puede comprobar facilmente que la suma de los numeros impares de la fila tres es 27=7+9+11, el cual es el cubo de 3, de igual forma puede comprobar para las demás filas.
Epistemología en la teoría de números
La comprobación de la multiplicación fue muy útil para los comerciantes y artesanos. A la hora de cerrar un trato era una "buena" forma de rectificar que las cuentas estuvieran bien y no se tratará de una estafa. A esto se le dio mucho uso durante un tiempo por parte de los contadores, pero después de un tiempo dejo de ser útil debido a que no siempre era correcto el pronóstico de la comprobación.
Geometría
Por el año 950, Abul Wefa escribió un libro titulado Kitab fi ma yahtaj ilayh al sani min al-amal al-handasiyya (Sobre las partes de la geometría que necesitan los artesanos), que suministra diversas clases de construcciones, muchas de las cuales se pueden realizar solo con regla y compás. Sin embargo, los árabes realizaron su construcción de secciones cónicas con estos utensilios básicos.Epistemología en la geometría
La geometría fue una herramienta muy útil para los artesanos, cuyas propiedades les ayudaban a crear jarrones y platos de forma geométrica, en la estructura de los edificios que llegaban a un punto de simetría que era muy placentero para la vista y entre otras. Después de la publicación del libro de Abul Wefa (Sobre las partes de la geometría que necesitan los artesanos) revoluciono el pensamiento de los artesanos con sus creaciones, la belleza era comparada con lo simétrico y lo proporcional, llegando así a unos hermosos mosaicos con figuras geométricas a base de solo regla y compás.
Demostración y Generalización del Teorema de Pitágoras
Haciendo click en la imagen te llevará a una demostración interactiva usando la herramienta de Geogebra.
Cultura y Arte

Los árabes fueron grandes receptores de las culturas precedentes:
- De la China, incorporó el papel, recurso que permitirá, en el futuro, multiplicar la información impresa; la brújula, instrumento que facilitaba la orientación geográfica diurna, y la pólvora, que alimentó la artillería en las futuras guerras.
- De la India adoptaron los números arábigos, que aprendemos desde la enseñanza básica que posibilitan las más primarias y fundamentales operaciones matemáticas.
- De los territorios griegos asimilaron el saber en distintas disciplinas, como la filosofía aristotélica, la geografía ptolomeica, que ubicaba a la Tierra como centro del sistema solar (Geocentrismo), la medicina descriptiva de las enfermedades de los griegos Hipocrátes y Galeno.
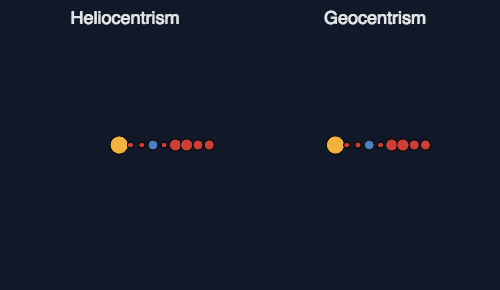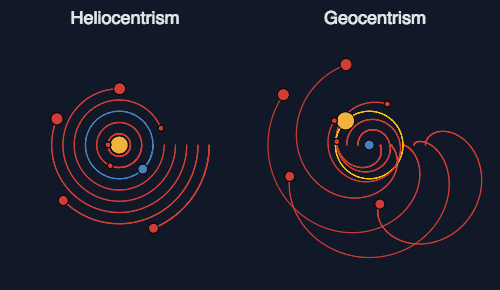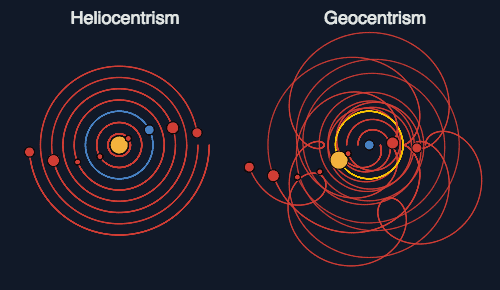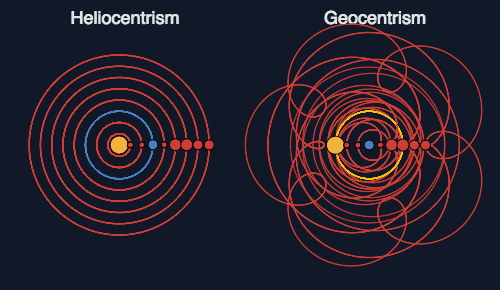
- De las tierras de Egipto y Mesopotamia, aprendieron las técnicas de riego artificial, y las de la construcción de obras hidráulicas.
Literatura
En la
literatura árabe el género más importante es la poesía.
En
el campo literario, lo más difundido son los cuentos condensados en Las mil y
una noches
- · Recopilación medieval en lengua árabe de cuentos tradicionales del Oriente Medio
- · El núcleo de estas historias está formado por un antiguo libro persa llamado Hazâr afsâna («mil leyendas»)
y
que ha sido recreada bajo nuevos lenguajes, como el de los de comics y el cine
de Disney.
A continuación te dejamos un pdf con algunos cuentos y también la película de disney Aladdín inspirada en el cuento árabe Aladino, de la colección de Las mil y una noches para ver online
(Da click a alguna imagen)
La Alhambra «al-Qal'a al-hamra» ('fortaleza roja')
 Es una ciudad palatina andalusí situada en Granada, en comunidad autónoma de Andalucía, España, consiste en un conjunto de palacios, jardines y fortaleza que albergaba una verdadera ciudadela dentro de la propia ciudad de Granada.
Es una ciudad palatina andalusí situada en Granada, en comunidad autónoma de Andalucía, España, consiste en un conjunto de palacios, jardines y fortaleza que albergaba una verdadera ciudadela dentro de la propia ciudad de Granada.
Su verdadero atractivo, como en otras obras musulmanas de la época, no solo radica en los interiores, cuya decoración está entre las cumbres del arte andalusí, sino también en su localización y adaptación, generando un paisaje nuevo pero totalmente integrado con la naturaleza preexistente.
Visita la Alhambra!
Con ayuda de Google Maps podrás navegar y visualizar algunos lugares de esta emblemática construcción.
Un aspecto interesante de la Alhambra y motivo por el cual resaltamos esta edificación árabe es la decoración en sus muros,
Para entender mejor debemos dirigirnos al mundo de las matemáticas
Para rellenar un plano con losetas (teselar el plano) de forma periódica, existen cuatro estrategias:
1.-Traslación. Es como si la nueva loseta que añadimos fuera una anterior desplazada a una nueva posición sin giros de ningún tipo.
2.-Rotación. La nueva loseta surge por el giro de una anterior con centro en algún punto determinado y con un ángulo concreto.
3.-Reflexión. Cada loseta nueva es la imagen especular de una anterior, con un eje de simetría dado.
4.-Simetría con deslizamiento. Se trata de una reflexión seguida de una traslación en la dirección del eje de reflexión.
Estas transformaciones se combinan entre ellas dando lugar a estructuras algebraicas que se denominan grupos de simetría plana o cristalográficos.
En 1891, el cristalógrafo ruso E.S. Fedorov demuestra que solo hay 17 grupos de simetría plana.
En 1891, el cristalógrafo ruso E.S. Fedorov demuestra que solo hay 17 grupos de simetría plana.
 |
| Click aquí si quieres conocer cada grupo |
En los adornos ornamentales de suelos y paredes de la Alhambra se pueden encontrar ejemplos de cada uno de los grupos cristalográficos planos.
Los creadores de los mosaicos de la Alhambra no podían conocer el teorema de clasificación de Fedorov ya que esta fue construida aproximadamente en el siglo XIII, y por lo tanto no conocían cuántos grupos de simetrías podían usarse para rellenar el plano con baldosas (teselación del plano), por eso resulta impactante que conocieran todos y cada uno de los 17 existentes.
ZONA DE JUEGOS
Ahora te dejamos unos cuantos juegos para que te diviertas y sigas aprendiendo aún más sobre la cultura Árabe.
 Con esta sopa de letras no solo te divertirás, si no que aprenderás un poco de la cultura árabe, sobre sus instrumento musicales y su agricultura. ¡Animate a conocer más sobre esta cultura!
Con esta sopa de letras no solo te divertirás, si no que aprenderás un poco de la cultura árabe, sobre sus instrumento musicales y su agricultura. ¡Animate a conocer más sobre esta cultura!
 Con esta sopa de letras no solo te divertirás, si no que aprenderás un poco de la cultura árabe, sobre sus instrumento musicales y su agricultura. ¡Animate a conocer más sobre esta cultura!
Con esta sopa de letras no solo te divertirás, si no que aprenderás un poco de la cultura árabe, sobre sus instrumento musicales y su agricultura. ¡Animate a conocer más sobre esta cultura!
Este juego consiste en identificar y relacionar la imagen de los personajes históricos de la civilización árabe y de las matemáticas árabes, con sus nombres. Animate a conocer como eran estas grandes mentes. ¡Que esperas!
Con este juego aprenderás sobre los grandes aportes que nos dejo está civilización, su historia, la matemática árabe y lo que aprendieron de otras civilizaciones. ¡Animate a jugar, diviértete aprendiendo!
Este juego consiste en identificar la hora exacta en cada reloj de sol. Será muy divertido aprender un poco el funcionamiento de este curioso artefacto, tal vez un día te sea útil.
Con este juego aprenderás sobre los grandes aportes que nos dejo está civilización, su historia, la matemática árabe y lo que aprendieron de otras civilizaciones. ¡Animate a jugar, diviértete aprendiendo!
Este juego consiste en identificar la hora exacta en cada reloj de sol. Será muy divertido aprender un poco el funcionamiento de este curioso artefacto, tal vez un día te sea útil.
Ahora un chiste y una adivinanza para que compartas con tus amigos:














No hay comentarios.:
Publicar un comentario