ESCUELA PITAGÓRICA

BIOGRAFÍA DE PITÁGORAS



MATEMÁTICAS EN LOS PITAGÓRICOS


EPISTEMOLOGÍA DE LOS NÚMEROS PARA LOS PITAGÓRICOS

Los números para los pitagóricos, les dan características a los números, el 1 por ejemplo es el que genera todo ya que según los pitagóricos con este puedo construir cualquier otro y además como la esencial del universo para ellos eran los números, entonces con el número 1 se podía generar todo, el diez también era esencial para ellos ¿pero por qué? Porque según ellos era la tetractys, numero con el cual hacían juramentos, además los cuatro primeros números contenían el secreto de la escala musical, y para los pitagóricos la música era fundamental, ya que ellos pudieron distinguir entre diferentes tonos a partir de algoritmos matemáticos.
LOS NÚMEROS
Los diez primeros números para los pitagóricos fueron muy importantes a estos los llamaron
LA DÉCADA O TETRACTYS
y les atribuyeron características místicas, en el siguiente vídeo, se presentaran algunas de los características de estos números.


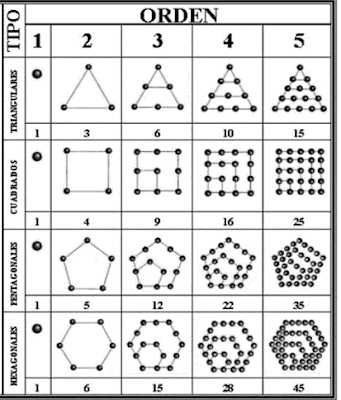
Los pitagóricos también clasificaron los números según su forma de la siguiente manera:


Ve al final de la página y JUEGA para que refuerces lo que haz aprendido!

EPISTEMOLOGÍA NÚMEROS POLIGONALES

Los números poligonales tras el análisis y la profundización sobre los números, como para ellos los números los representaban por piedrecillas, vieron que con ellos podrían formar polígonos regulares y de esto se obtuvo los números poligonales, así estuvieron las propiedades de estos, como se observó en la página principal de los pitagóricos.
NÚMEROS POLIGONALES
Los pitagóricos solían representar los números mediante puntos en un pergamino o piedrecillas en la arena y los clasificaban según las formas poligonales de estas distribuciones de puntos.

La asociación del número con  la forma geométrica permitió a los pitagóricos la representación visual de los números. Confirieron a los números propiedades y relaciones entre ellos que son completamente independiente de todo el simbolismo introducido para representarlos.

Los números poligonales aparecieron en los albores de la escuela pitagórica como un elemento esencial de su misticismo numérico:
"No sólo las cosas son en esencia números sino que los números son concebidos como cosas"







OBSERVE!
Para cada orden los números poligonales del mismo tipo forma una progresión aritmética  cuya diferencia es el numero triangular de orden previo:

q 3,4,5,6,…progresión  aritmética de diferencia 1.
q6,9,12,15… progresión aritmética de diferencia 3.
q10,16,22,28… progresión aritmética de diferencia 6.
q………………


PROPIEDADES
1.T(n)+T(n)=n(n+1)→Número oblongo
2. Gnomon

3.C(n)=T(n)+T(n-1)

4.P(n)=T(n)+2T(n-1)
5.Hex(n)=T(n)+3T(n-1)

6. Generalización
P_r (n)=T(n)+(r-3)T(n-1)
Para observar las triangulaciones de los poligonos superiores a los anteriores da click aquí.

Ve a la página de juegos y y aplica lo que aprendiste. Sobre este tema, juega el juego #3.

SOLIDOS PITAGÓRICOS



CUBO
DODECAEDRO
OCTAEDRO
ICOSAEDRO
TETRAEDRO

Información sobre los sólidos pitagóricos

NOMBRE
N
M
C
V
A
TETRAEDRO
3
3
4
4
6
CUBO
4
3
6
8
12
OCTAEDRO
3
4
8
6
12
 DODECAEDRO
5
3
12
20
30
ICOSAEDRO
3
5
20
12
30

N=Número de aristas en cada cara.
M: Número de aristas en cada vértice.
C: Número de caras.
V= Número de vértices.
A= Número de aristas

TEOREMA DE PITÁGORAS


(AB)2= (CA)2+ (BC)2

Este teorema, pitàgoras no lo descubriò. En otras culturas como la egipcia ya utilizaban las ternas pitagóricas para las labores de la agricultura.
Pitàgoras demostrò el teorema de pitàgoras, fue el primero, pero en la actualidad ya hay mas de 300 demostraciones de dicho teorema.

 ¿En dónde está el teorema de pitágoras?



LA SECCIÓN ÁUREA


"Se dice que un segmento está dividido en media y extrema razón cuando el segmento total es a la parte mayor como la mayor es a la menor"

Como se muestra continuación:





Tomando AB=1 y BC=x, la razón áurea se expresará de la forma:


Al número x se le llama el número de oro. Tradicionalmente se le representa por la letra griega φ.



LA DIVINA PROPORCIÓN

LOS INCONMENSURABLES


EPISTMOLOGÍA DE LOS INCONMENSURABLES
Los inconmensurables el descubrimiento de lo irracional, del Alagón fue producto de los Pitagóricos fue un hombre llamado Hipaso de Metaponto quien dio a luz la idea del número racional, a esto llego estudiando la relación entre la diagonal y el lado de un triángulo, el vio que no había una unidad que me relacionara estos dos segmentos, pero el descubrimiento de lo irracional también pudo a ver sido por el numero áureo ya que este es esencial cuando estudiaban el símbolo que los identificaban, esto es el pentagrama místico. Con el surgimiento de los irracionales toda la doctrina de los pitagóricos comenzó a caer, y quien dijo que por el descubrimiento que hizo un mismo pitagórico.

Observa la siguiente historieta, se cuenta como se cree que surgieron los inconmensurables.

La grandeza del teorema de Pitágoras  y la mágica belleza del pentagrama místico fueron dos caballos de Troya para la geometría griega, porque llevaban en su interior el germen de la profunda crisis de la secta pitagórica. La comunidad Pitagórica se vio gravemente alterada por el descubrimiento porque prácticamente demolía la base de la fe pitagórica en los números enteros. La creencia de que los números podían medirlo todo era una simple ilusión. Quedaba así eliminada de la geometría la posibilidad de medir siempre con exactitud. Se había descubierto la magnitud inconmensurable, lo irracional, el alagon, que provocaría una crisis en la historia de las matemáticas.

Se dice que pudo surgir cuando Hipaso un Pitagórico estaba aplicando el teorema de Pitágoras a un triángulo rectángulo isósceles de lado 1, donde apareció Raíz de dos. O quizá también estudiando su propio símbolo el pentagrama místico, cual era relacionando la diagonal con uno de sus lados.

A continuación se muestra como es la demostración geométrica de la irracionalidad de raíz de 2



COSMOLOGÍA PITAGÓRICA

Era tanto la veneración del número diez para los pitagóricos que fue una clave para como creían que era la configuración del universo, para ellos era un sistema astronómico no geocéntrico, además los pitagóricos afirmaban que los cuerpos que se mueven en torno de los cielos son diez, pero al ser nueve solamente visibles, se inventan, el décimo, la "anti-tierra"  los pitagóricos afirmaban que en el centro esta el FUEGO, y que la tierra es uno de los astros que se mueve al rededor de este.

Los nueve cuerpos celestes  eran:
  1. La Tierra.
  2. La anti-Tierra.
  3. La Luna.
  4. El Sol.
  5. Mercurio.
  6. Marte.
  7. Venus.
  8. Saturno.
  9. Júpiter.

HORA DE REÍR!!!

LA MÚSICA PITAGÓRICA


Pitágoras estudio, quizá por primera vez las leyes cuantitativas de la acústica y pues, fue el primero en encontrar una correlación entre los sonidos armónicos y los números.

Nota: los sonidos armónicos son aquellos cuya manifestación simultanea origina una sensación agradable a nuestro oído por ejemplo: el tono, la octava, la quinta y la cuarta.

En toda combinación armónica las longitudes relativas de las cuerdas pulsadas están en una razón de números enteros, que se sintetiza en el esquema siguiente, llamado sistema de Pitágoras.



Para entender de donde sale cada uno de estos valores, debemos recordar, que la construcción de la escala musical se fundamenta en la quinta perfecta de razón 3/2. Además, de que se inicia con una nota base, que en nuestro caso sera DO.

EL monocordio

 A Pitágoras se le atribuye la invención del monocordio. Este artilugio consistía en una simple cuerda musical, la cual se encontraba tendida sobre una tabla, con un puente móvil deslizable entre cuerda y tabla, para obtener cuerdas de diversa longitud.



La cuerda tiene una longitud L. Al pulsar la cuerda en su totalidad , se produce el tono(o nota base); al ubicarse el puente móvil en 3/4(L) corresponde a la cuarta nota con respecto a la nota base; al moverse el puente móvil en 2/3(L) corresponde a la quinta nota con respecto a la nota base; por último, colocando el puente móvil en 1/2(L) corresponde la octava de la nota.

Armonía de las esferas 

 Es la quintaesencia de la belleza en la explicación del cosmos divino, armonizado de forma fascinante por la concordancia de las proporciones aritméticas  y musicales, que llevadas al universo entero, determinarían que los cuerpos celestes emitieran en sus movimientos unos tonos musicales armoniosos, cuya combinación produciría una maravillosa melodía.
González, P. (2001). Historia de las matemáticas.

A JUGAR!


JUEGO # 1

 SOPA DE LETRAS
En el siguiente juego debes buscar algunas palabras relacionadas con la biografía y filosofía de Pitágoras




JUEGO # 2

RELACIONA
En el siguiente juego relaciona cada número con su significado para los pitagóricos

JUEGO # 3
JUEGO DE NÚMEROS POLIGONALES
En el siguiente juego podrá aplicar lo que aprendió de los números poligonales, este consiste en unas preguntas sobre el tema

JUEGO # 4
Responde la pregunta







                       

HECHOS EPISTEMOLÓGICOS

  • MÚSICA


QUIERES VER Y APRENDER A MANEJAR UN MONOCORDIO, VE AL SIGUIENTE LINK Y DESCARGA LA APLICACIÓN TE ASEGURO QUE DISFRUTARÁS Y APRENDERÁS MUCHO. 


  •      TEOREMA DE PITÁGORAS

El teorema de pitágoras es uno de los teoremas más lindos de Matemáticas, aunque ya lo habían utilizado antes que Pitagóras, Pitagóras fue el primero que le dio una demostración formal. El teorema lo podemos encontrar en muchos situaciones de la vida diaria, a continuación mostraremos unos ejemplos:

  •      LOS INCONMENSURABLES

HISTORIA Y EPISTEMOLOGÍA

  • NÚMERO ÁUREO 
  •   
REFERENCIAS
qGonzáles Urbaneja, PM, Pitágoras el filósofo del número, Barcelona, Editorial Nivola.

No hay comentarios.:

Publicar un comentario

Suscribirse a: Entradas (Atom)