MATEMÁTICA HELENÍSTICA


Historia

Alejandro III de Macedonia, más conocido como Alejandro Magno o Alejandro el Grande, nació en 356 a.C. Su padre era Filipo II, rey de Macedonia de a.C a a.C., quien poseía una gran habilidad para la guerra y estableció al ejército macedón como una de las principales fuerzas militares del mediterráneo.

Su campaña conquistadora tuvo su punto más alto cuando junto con Alejandro, que tenía sólo 16 años en ese momento, lideraron la conquista de Atenas y tomaron control de toda Grecia. La invasión de Macedonia fue bien recibida por los griegos que habían estado bajo control persa más de un siglo. Los macedonios eran culturalmente muy similares a los griegos. Por ejemplo, adoraban algunas de los mismas deidades y su idioma era muy parecido al hablado por los griegos.

Filipo decidió que los griegos y los macedonios lucharían juntos para conquistar todos los territorios del imperio persa, es decir, Egipto, Asia Menor y Mesopotamia. Sin embargo, murió asesinado en Macedonia antes de que iniciara su campaña de conquista. Tras la muerte de Filipo, Alejandro tomó el mando del poderoso ejército macedón y siguiendo los pasos de su padre comenzó la conquista de territorios. Alejandro resultó ser
incluso mejor general que su padre.

Lideraba desde el frente a sus tropas y planeaba estrategias de de batalla que le permitieron superar ejércitos mucho más numerosos. Alejandro continuó conquistando sin detenerse por 13 años consecutivos. Cuando su campaña terminó, Alejandro Magno y su ejército se habían tomado los territorios ya mencionados y además una gran parte de la India. 


Tras su regreso, los guerreros macedonios entraron a Babilonia que ahora estaba bajo su control. Los babilonios aceptaron a Alejandro como su rey y empezaron a generarse tensiones entre los generales macedonios y la nobleza babilónica. El deseo de Alejandro era que se realizara una integración de las dos culturas y tomó medidas, como obligar a sus hombres a contraer matrimonio con mujeres de babilonia, para que se cumpliera.

Alejandro III de Macedonia, murió en el 323 a.C. en Babilonia donde contrajo una fiebre cuya causa es desconocida que finalmente le quitó la vida. Al morir, dejó una viuda embarazada y un imperio más grande que cualquier otro antes.

Como el hijo de Alejandro no había nacido, y no había ningún familiar que pudiera heredar el poder, los generales de su ejército pasaron los siguientes 20 años disputándose el control de los territorios. Uno de ellos era Ptolomeo I Sóter, quién era uno de los guardaespaldas de Alejandro y desde niños habían sido cercanos (incluso hay quienes sostienen que Ptolomeo era un hijo ilegítimo de Filipo). En la repartición, Ptolomeo se quedó con los territorios egipcios. 

Ptolomeo II con su atuendo de faraón.
Decidió que la capital de su reino sería la ciudad de Alejandría, en la costa del mar mediterráneo, próximo al delta del río Nilo. La dinastía ptolemaica se establecería en Alejandría por más de 250 años, llegando a su fin cuando los romanos bajo el mando de Julio César tomaron control. Durante los reinados de los primeros Ptolomeos (Todos los reyes tomaron el mismo nombre) la ciudad vio un florecimiento económico e intelectual incomparables. La abundancia de papiro facilitó la formación del conjunto de documentos y textos académicos más grande que se había visto, la Biblioteca de Alejandría. Allí se formaron los matemáticos de los que vamos a hablar.



Filosofía



La escuela filosófica peripatética fue fundada por Aristóteles en Macedonia en el siglo IV a.C. Su nombre proviene del hecho que sus miembros preferían deambular mientras discutían sus ideas filosóficas y científicas.  
Básicamente, las ideas que mantenían y desarrollaban los peripatéticos fueron propuestas por Aristóteles, quien es considerado uno de los filósofos más importantes de la Antigua Grecia junto con su maestro Platón.


Aristóteles escribió sobre física, política, ética, biología y, por supuesto, filosofía. Como muchos de sus antecesores consideraba que toda la materia estaba compuesta de combinaciones de 5 elementos fundamentales: agua, aire, tierra, fuego y éter. Además, pensaba que cada uno de los elementos fundamentales tenía un lugar natural y que los objetos poseían una tendencia a moverse hacia su lugar natural. Por ejemplo, Aristóteles pensaba que el fuego estaba más arriba de los cielos, pues las llamas tienden a subir, o cuando llueve el agua cae del cielo sobre la tierra, o que si arrojamos tierra en el océano está se hundirá hasta el fondo.
Aristóteles es considerado el primer biólogo. Ciertamente tenía una afinidad por esta ciencia. Su meta era entender al hombre y su razón de ser. Observó con mucho cuidado grandes cantidades de animales y clasificó muchas especies según sus características físicas. Esto lo llevó a la idea de que hay distintos tipos de ser y que estos tipos de ser tienen distintos tipos de alma. Entonces hay almas vegetativas, almas animales y almas racionales. Para Aristóteles el ser humano es el único ser que poseía las tres almas (más específicamente el único que posee alma racional).
La palabra ética fue acuñada por Aristóteles para referirse al área filosófica estudiada por Platón y Sócrates que trata de establecer qué es una vida virtuosa. En el período helenístico esta disciplina tomó una gran relevancia y por los próximos 300 años después de Aristóteles las preguntas concernientes a lo ético estuvieron al frente de la filosofía. En respuesta a la escuela peripatética surgirían dos grandes escuelas filosóficas: el estoicismp y el epicureísmo.

Euclides

Euclides vivió alrededor del año 300 a.C. en la ciudad de Alejandría. Además de esto no sabemos casi nada sobre la vida de él. Sin embargo, es recordado por ser el autor del libro de matemáticas más famoso de la historia, Los Elementos. Se dice que este libro es el segundo que más ha sido publicado en la historia de la humanidad, el primero siendo la Biblia.
En Los Elementos, Euclides expone las matemáticas que habían sido desarrolladas por generaciones anteriores de matemáticos griegos en una forma completamente rigurosa. En este libro se trata geometría plana, teoría de proporciones, teoría de números, teoría de irracionales y geometría sólida.


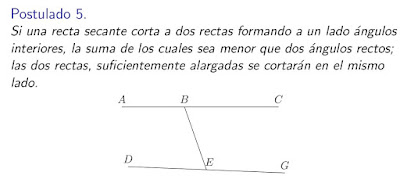
Al inicio de Los Elementos, Euclides da 5 postulados que establecen las reglas para crear las construcciones que permitirán poner sobre una base lógica los resultados matemáticos. De los 5 postulados, el más complicado es el quinto.


De hecho, muchos matemáticos posteriores que estudiaron la obra de Euclides trataron de demostrarlo pero fue en vano. Sólo en el siglo XIX se entendió que negando este postulado se obtenían otros dos sistemas geométricos lógicamente consistentes.
Euclides usa este postulado por primera vez en la proposición 27 del Libro I, mientras que todos los otros 4 axiomas se usan en casi todas las demostraciones. Por lo que se sospecha que Euclides era consciente de la complejidad del quinto postulado pero no pudo encontrar una demostración para hacerlo en cambio una proposición.
Euclides usó la misma estructura para prácticamente todas las demostraciones. En la siguiente imagen se ilustra con un ejemplo dicha estructura.



El estilo adoptado por Euclides para Los Elementos es uno en el que se valora la presentación y que toda afirmación pueda deducirse del contenido que la precede. Algunos historiadores de las matemáticas griegas llaman este estilo sintético. Esta tradición sigue manteniéndose hoy en día en muchos artículos y libros de matemáticas. Inclusive este estilo llamó la atención del filósofo Baruch Spinoza en el siglo XVII, quién intentó axiomatizar la ética y escribir un tratado sintético sobre cómo llevar una vida virtuosa.
Los tratados sintéticos son muchas veces la manera preferida de los matemáticos para comunicarse (La encuentran eficiente, ordenada y elegante). Sin embargo, tiene una deficiencia y es que no muestra la forma en que el autor llegó a su idea. Esto tiene el efecto de que en tratados sintéticos (en el sentido griego) las demostraciones pueden parecer magia y dejar confundido al lector con poca experiencia.
La contraparte de la síntesis se llama análisis y consta de suponer que se cumple lo que se quiere demostrar y buscar deducir algo que se conozca que sea equivalente. Euler fue un matemático reconocido por siempre explicar el proceso por el cual encontraba solución a sus problemas. El problema de incluir el análisis en un tratado matemático es que lo lleva a ser desorganizado y el orden de presentación de las ideas se pierde.

Geometría Plana

Los libros I al IV de Los Elementos tratan sobre geometría plana. Entre los resultados más destacados se encuentra el Teorema de Pitágoras. Está incluido al final del Libro I, cuando Euclides está desarrollando algo de teoría de áreas. Aparte de esta proposición, el Libro I incluye teoremas básicos sobre triángulos, rectas paralelas y paralelogramos.

 Demostración de Teorema de Pitágoras Geogebra.
En el Libro II, Euclides desarrolla una teoría de áreas que le permite, en esencia, resolver varios tipos de ecuaciones cuadráticas ( ). En el Libro III, se ocupa con la geometría de círculos, mientras que en el libro IV decide aplicar lo que ha expuesto en los tres primeros libros para construir polígonos inscritos y circunscritos a un círculo dado.


Teoría de Proporciones
En el Libro V, Euclides presenta la teoría de proporciones de Eudoxo. Eudoxo de Cnido fue un matemático griego de gran influencia. Sin embargo, su trabajo sólo ha llegado a nosotros a través del crédito que le han dado matemáticos posteriores como Euclides o Arquímedes.
La teoría de proporciones tenía un inmenso valor en las matemáticas de la antigüedad. No sólo porque fue precursora de la trigonometría, sino en la misma geometría porque permitió la comparación de relaciones que guardan las diferentes figuras geométricas entre sí.
Por ejemplo, si se tiene un círculo con área A y circunferencia C, y un cuadrado con área D y un triángulo con perímetro P, entonces se puede encontrar la proporción A:D y la proporción C:P. Estas dos proporciones son comparables aunque se refieran a dos cosas muy distintas.


Basado en esta teoría, Euclides desarrolla sus aplicaciones a la geometría plana en el Libro VI donde obtiene muchos resultados de semejanza de figuras geométricas.


Teoría de Números
En los Libros VII, VIII y IX, se presenta la teoría de números que se cree que era conocida por los pitagóricos o al menos por los platónicos. Contiene varios resultados muy famosos e importantes de esta área de las matemáticas.


Por ejemplo, está el algoritmo de la división, la demostración de la infinitud de los números primos, una proposición respecto a la factorización de ciertos números en números primos, una fórmula para números perfectos pares, la fórmula cerrada de la serie geométrica entre muchas otras.

Teoría de Irracionales
En el Libro X, se tratan los números irracionales, o los inconmensurables con la unidad. Es una mezcla de teoría de números y teoría de proporciones. Es el libro más extenso de todos Los Elementos y fue muy importante en su época. Sin embargo, las limitaciones de la geometría euclidiana no permitieron desarrollar una verdadera teoría de irracionales, pues los únicos irracionales con los que trataron los griegos fueron los construibles, es decir, aquellos que partiendo de figuras con magnitudes racionales se pueden construir con regla y compás. Resulta que estos números tan sólo contienen a los racionales, sus raíces cuadradas y combinaciones de estas como $\sqrt{2}+\sqrt{3}$, $\sqrt{1+\sqrt{2 + \sqrt{5}}}$, etc.
Aplicación para explorar inconmensurables.

Geometría Sólida

En los últimos tres libros. Euclides desarrolla la geometría sólida culminando con la construcción de los cinco sólidos platónicos y la demostración de que no puede existir ningún otro sólido regular.

Para conocer más sobre sólidos platónicos, haz clíck aquí.


Para finalizar esta sección sobre Euclides, en el siguiente link se puede encontrar un juego llamado Euclidea es cual es muy recomendado.

https://www.euclidea.xyz

Aristarco

Aristarco de Samos, fue un matemático helenístico que usó la geometría de Euclides para realizar estimaciones y cálculos aproximados que le permitieran construir un modelo del universo bien fundamentado en las matemáticas. Por desgracia, su trabajo fue rechazado por la comunidad intelectual de su lugar y tiempo y sus logros fueron olvidados por mucho tiempo. En el siguiente video se encuentra una entretenida charla sobre Aristarco.

En su libro Sobre los Tamaños y Distancias del Sol y la Luna, Aristarco desarrolló su modelo cosmológico partiendo de 6 hipótesis.


  1. La Luna recibe su luz del Sol.
  2. La Luna en una órbita circular cuyo centro está en la Tierra.
  3. Cuando exactamente la mitad de la Luna está ilumninada y la otra mitad oscura, se forma un ángulo de 90° entre la Tierra, la Luna y el Sol.
  4. En este momento (igual que en la hipótesis 3), el ángulo que se forma en la Tierra es de 87°.
  5. La sombra de la Tierra es dos veces más grande que la Luna, en el plano en el que la Luna la cruza durante un eclipse lunar.
  6. La porción del cielo que la Luna cubre en cualquier momento es igual 0.5°

Aristarco vino a estimar basándose en estas suposiciones que el Sol era 19 veces más grande que la Luna, pero que está 19 veces más lejos de la Tierra que la Luna. Luego, a pesar de que el Sol es mucho más grande que la Luna, en el cielo ambos tienen aparentemente el mismo tamaño.

Esta estimación estaba obviamente errada, pero se debe a que los cálculos de Aristarco no eran los mejores. Hay que tener en cuenta que no se tenían muchas mediciones precisas en áquella época. 

Para explorar la gran diferencia que hace un pequeño cambio en el ángulo al que hace referencia la hipótesis 6, haz clíck en este enlace.

De todas maneras, la aplicación de Aristarco de las matemáticas a la astronomía comenzaron una larga relación entre estas dos disciplinas que hoy en día sigue tratando de responder preguntas cada vez más complicadas sobre nuestro Universo.

La siguiente imagen muestra cómo cambia la distancia de la Tierra (o la Luna) al Sol cuando varíamos el ángulo en la Tierra entre 87° (la suposición de Aristarco) y 89°51', una medida más precisa de dicho ángulo. Se observa que la magnitud varia en crece de un 2000%, esto es porque las funciones trigonométricas secante y tangente tienen una discontinuidad infinita al aproximarse a 90°.




Arquímedes


Uno de los más grandes matemáticos de la historia. Su trabajo ha dejado supremamente impresionados a los historiadores de las matemáticas que lo han estudiado. En su época fue reconocido por sus inventos mecánicos que fueron de gran utilidad para la guerra y la agricultura. Pero Arquímedes consideraba que su obra importante eran sus matemáticas.


Desarrolló varias ideas importantes de la mecánica como equilibrio, centro de gravedad y la fuerza de empuje en el principio arquimediano de los fluidos. En sus descubrimientos matemáticos se encuentra la determinación de los tamaños de una gran cantidad de magnitudes geométricas (el área de un círculo, volumen de una esfera, por ejemplo). Muchos de estos problemas habían eludido a los antecesores de Arquímedes, y fue él quién cálculo muchos de estos valores y no sólo eso sino que demostró que sus cálculos eran correctos.


Arquímedes consideraba que su mejor descubrimiento había sido la relación entre las áreas y los volúmenes, de una esfera y un cilindro circunscrito a ella. Por eso pidió que en su tumba se mencionara este resultado con un diagrama. Hace mucho tiempo que se desconoce el lugar donde yacía el cuerpo de este gran pensador, pero los matemáticos modernos decidieron rendir homenaje a Arquímedes.

 En otro de sus sorprendentes y llamativos descubrimientos matemáticos, Arquímedes considero la espiral que se genera como se ve en en la siguiente animación:

Esto tiene una importancia epistemológica, pues Arquímedes se separa de los métodos euclidianos y considera en cambio la geometría de una curva generada por un mecanismo abstracto. En matemáticas modernas, estas curvas se representan por ecuaciones paramétricas, en el caso de la espiral arquimediana es conveniente usar coordenadas polares. La ecuación que describe a la espiral es $r = b*\theta$, donde $b >1$.


 Este tipo de curvas se siguieron estudiando durante la antiguedad y la modernidad. Muchas vienen inspiradas de problemas de la mecánica como las cicloides y las catenarias. Arquimedes, halló usando el método de exhausción de Eudoxo el área de muchas figuras, entre ellas, el área encerrada por la primera revolución de esta espiral. Encontró que es exactamente igual a un tercio del área del círculo que tiene radio igual al radio final de la primera revolución.

No sólo precedió al cálculo integral encontrando áreas de estas figuras relativamente complicadas. En el caso del espiral el área es aproximada por una partición de sectores circulares. Si Arquímedes hubiera intentado aproximar el área por medio de figuras rectilíneas, la aproximación habría sido mucho más complicada. Con toda seguridad él era consciente de este hecho y por eso habiendo encontrado el área del círculo previamente,  usó ese resultado para resolver el de la espiral. Esto es muestra de lo recursivo y genial que era este matemático de hace 2000 años.

La medalla Fields es un premio que se entrega a los matemáticos que hayan realizado el mejor trabajo. El premio se entrega cada 4 años a 4 matemáticos menores de 40 años.
A la izquierda está la parte frontal de la medalla con una imagen de Arquímedes. A la derecha está la parte posterior con una representación de la tumba de Arquímedes.

El método de Arquímedes para aproximar $\pi$, de Arquímedes fue el mejor durante casi 2000 años. Sólo fue superado con el descubrimiento de las series convergente y de técnicas de aceleración de convergencia, en el siglo XVIII.

Enlaces






Eratóstenes

Eratóstenes de Cirene, fue un científico helenístico. Se formó en Alejandría y correspondía con Arquímedes quien lo estimaba mucho como amigo y como intelectual. Es conocido principalmente por haber estimado la circunferencia de la Tierra. También estimó el ángulo de inclinación de la Tierra sobre su eje de rotación tratando de explicar las estaciones. Fue el primer geógrafo, hizo mapas y estudió los distintos climas. Trató de establecer una cronología para los eventos del pasado. 


En matemáticas, inventó un algoritmo para encontrar los números primos hasta una cota predeterminada. El algoritmo se conoce como la criba de Eratóstenes.

By SKopp at German Wikipedia - Own work, Original image at Image:Animation_Sieve_of_Eratosth.gif, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2810935




Suscribirse a: Entradas (Atom)